It feels like 2010 again - the bloggers are debating the proofs for the existence of God. I found these much less interesting after learning about Max Tegmark’s mathematical universe hypothesis, and this doesn’t seem to have reached the Substack debate yet, so I’ll put it out there.
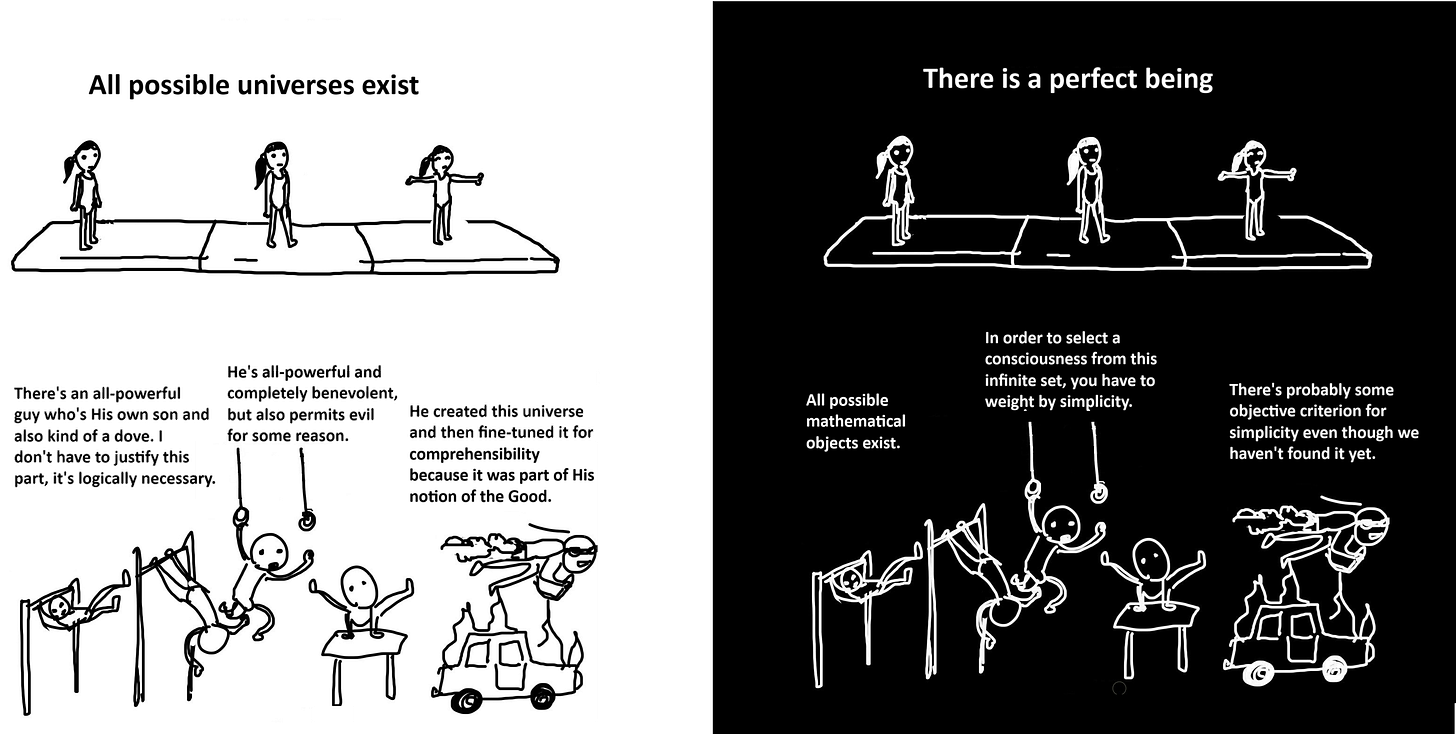
Tegmark’s hypothesis says: all possible mathematical objects exist.
Consider a mathematical object like a cellular automaton - a set of simple rules that creates complex behavior. The most famous is Conway’s Game of Life; the second most famous is the universe. After all, the universe is a starting condition (the Big Bang) and a set of simple rules determining how the starting condition evolves over time (the laws of physics).
Some mathematical objects contain conscious observers. Conway’s Life might be like this: it’s Turing complete, so if a computer can be conscious then you can get consciousness in Life. If you built a supercomputer and had it run the version of Life with the conscious being, then you would be “simulating” the being, and bringing it into existence. There would be something it was like to be that being; it would have thoughts and experiences and so on.

Tegmark argues this is also true if you don’t build the supercomputer and run it. The fact that the version of Life with the conscious being exists in possibility-space is enough for the being to in fact be experiencing it.
By existing, you are a random draw from the set of possible conscious beings. You can’t make a random uniform draw from an infinite set, but the accepted solution is some kind of nonuniform draw weighted by simplicity. So even though every possible mathematical object exists, simpler ones exist more. Most conscious beings exist in very simple universes, ones that (like Life) are just a few short rules which produce surprisingly complex behavior.
(Note that the universe itself doesn’t have to be simple - it can have ships, shoes, sealing wax, cabbages, kings, and the like. It just has to be generated from a simple ruleset - ie you can write the laws of physics on a single chalkboard.)
AFAICT, this obviates the top five classical arguments for God:
Cosmological: Why is there something rather than nothing? Because mathematical objects are logically necessary, and “existence” is just what it feels like to be a conscious observer on the inside of a mathematical object.
Fine-tuning: Why are the values of various cosmological constants exactly perfect for life? Because there are zillions of mathematical objects, but only the ones capable of hosting life do so. Therefore, a conscious observer inevitably finds themselves inside a mathematical object capable of hosting life.
Argument from comprehensibility: why is the universe so simple that we can understand it? Because in order for the set of all mathematical objects to be well-defined, we need a prior that favors simpler ones; therefore, the average conscious being exists in a universe close to the simplest one possible that can host conscious beings.
First cause argument: All things must have a cause. What is the cause of a cellular automaton’s starting position? There is none within the automaton itself. If a human is simulating the automaton on a computer, there’s some sense in which the cause is in the human’s world - it’s whatever made the human choose to simulate it from that starting position instead of another. But when you consider the automaton as a mathematical object, it doesn’t need a cause; you can start an automaton any way you want; they’re all just different mathematical objects. If we were selecting for simplicity, we would expect for most objects to start as a singularity and then explode outward (hmmmmm…)
Teleological argument: Why does the world have interesting structures like living things? There is no penalty for realized complexity, only for complexity of the starting laws. Given that we’re conscious beings, the world must be complex enough to contain conscious beings.
The only hole in this theory is that it’s hard to objectively define “simplicity” (it’s easy within a programming language - shorter programs are simpler - but how does the universe decide which programming language to use?) But I don’t think that makes it worse than its theist competitor. It’s pretty hard to objectively define God! If God is an infinitely good, infinitely powerful being, it seems like we need to start with a definition of “good” and “powerful” to limit ourselves to a single God in possible-deity-space. I would rather accept the challenge of defining “simplicity”, even though I’m not sure how to do this.
(also, since God is supposedly infinitely simple, you might still need an objective definition of simplicity anyway!)
Speaking of defining simplicity, it seems like, in order to decide between atheistic vs. theistic accounts of creation, all we need to do is determine which theory is simpler. I predict some disagreement here:
But also, I think nitpicking specific holes misses the point. In Miles Donahue’s post on these arguments, he says he can’t really think of a great response to fine-tuning, but suspects that the terrain is too difficult and unexplored to give up and say God is the only answer. This answer was first proposed c. 2014. I only know about it because Tegmark writes about AI and x-risk enough that some of my friends are big fans. If it’s true, it’s true. But if it’s false, then the very fact that we waited this long to get it suggests that there are lots of possible godless explanations of the universe (that satisfy the supposed proofs of God’s existence) that we haven’t thought of yet. Instead of taking the proofs at their word that it’s God or nothing, we may fairly expect many undiscovered third alternatives.



Share this post